AB测试里的统计学 PART 2 #
统计学在A/B测试中至关重要,它提供了评估测试结果可信度、确定显著性、计算样本量以及分析和解释数据的方法,从而帮助决策者做出基于数据的明智决策。本文将聚焦于出现在A/B测试中的统计学,为科学的实验过程,可靠的实验结论打下基础。
1. 样本大小计算 #
这里的样本计算出来是每组最少需要的样本量。如果比较两组,那么需要的最少样本量就是 \(N = 2 \times n\)。
1.1 公式计算 #
$$ 双尾实验:n = (Z_{1-\frac{\alpha}{2}} + Z_{1-\beta})^2 \frac{\sigma^2_{pooled}}{\triangle^2} $$
$$ 单尾实验:n = (Z_{1-\alpha} + Z_{1-\beta})^2 \frac{\sigma^2_{pooled}}{\triangle^2} $$
其中:
-
一般情况下会使用双尾实验
-
\(Z_{1-\frac{0.05}{2}} = 1.96\), \(Z_{1-0.2} = 0.84\) (\(\alpha = 0.05,\beta=0.2\) )
-
pooled 的意思是两个 variance 相加,\(\sigma^2_{pooled} = \sigma^2_B + \sigma^2_A\)
-
均值类:\(\triangle^2 = (\bar{X}_B-\bar{X}_A)^2\);比率类:\(\triangle^2 = (\hat{P}_B-\hat{P}_A)^2\)
-
Estimate of variance:
比率类(Proportion) 均值类(Mean) one-sample \(\sigma^2 = P(1-P)\) \(S^2=\frac{\sum{(x_i-\bar{X})^2}}{n-1}\) two-sample \(\sigma^2_{pooled} = P_B(1-P_B)+P_A(1-P_A)\) \(S^2_{pooled} = 2*S^2_A\) - n-1: unbiased estimation of the variance
- \(2*S^2_A\) 是因为在开始实验前,并不知道实验组的 variance
-
例子:
- 已知 \(MDE = 10 \% \), \(\bar{X}_A=10\), \(\sigma^2_A=20\), 求最小样本大小是多少?
- 假设\(\alpha = 0.05, \beta = 0.2\)
- \(\bar{X}_B=\bar{X}_A \times (1 + MDE/100) = 10(1+0.1) = 11\)
- \(n = (1.96+0.84)^2\times \frac{2\times 20}{(11-10)^2} \approx 314\)
- 由此可推算出一组最少需要314个样本,两组则最少需要618个样本。
| \(\alpha\) | \(Z_{1-\frac{\alpha}{2}}\) | \(Z_{1-\alpha}\) | · | \(1-\beta\) | \(Z_{1-\beta}\) |
|---|---|---|---|---|---|
| 0.01 | 2.58 | 2.33 | · | 0.8 | 0.84 |
| 0.025 | 2.24 | 1.96 | · | 0.9 | 1.28 |
| 0.05 | 1.96 | 1.64 | · | 0.95 | 1.64 |
| 0.10 | 1.64 | 1.28 | · | 0.99 | 2.33 |
1.2 简化版公式 #
$$ n \approx 16 \times \frac{\sigma_A^2}{\triangle^2} $$
其中:\(16 \approx (Z_{1-\frac{\alpha}{2}} + Z_{1-\beta})^2 \times 2\), (当 \(\alpha=0.05\) & \(\beta=0.2\)时)
1.3 在线计算器 #
可以通过在线计算器,计算出最小样本的大小 https://www.evanmiller.org/ab-testing/sample-size.html
相关参数的解释:
- Baseline conversion rate:对照组的次日留存率、点击率、渗透率等等比例值;
- MDE可以参考 上篇文章
- Power 和 \(\alpha\) 大部分情况会分别设置为:\(80\%\) 和 \(5\%\)
2. 实验时间计算 #
$$ 实验时间 = \frac{N}{每天总流量 \times 划分给实验的流量占比(\%)} $$
- 其中N=所有组的样本大小总和
- 如何选择我们需要观察的用户?
- 比如我们观察的指标是每天级别的,第一天选中了用户A,第一天观察完后,接下来就不能再观察A了
- 第二天需重新选择用户,并且要把第一天的排除掉
- 以此类推,以满足样本的独立性
- 时间不能短于7天,要包含工作日和周末
- 考虑到时间成本,也最好不要长于两周,除非流量太小了
- 最好控制在1-2周,这是比较常见的时间范围去做AB测试
3. 其他相关的统计知识点 #
3.1 验证数据的正态分布 #
-
直方图:查看直方图是否形成一个钟形的曲线
-
Q-Q图:判断点和线是否在同一条线上
-
相关的统计检验方法:
- Shapiro-Wilk
- Kolmogorov-Smirnov
- 这两个实验的原假设:数据集是来自于正态分布,备择假设:数据集不来自于正太分布
- 如果P-value小于\(\alpha\),则拒绝原假设认为它大概率不是正态分布;但是如果P-value大于\(\alpha\),则不能拒绝原假设,并结合其他的办法去判断数据是否是正态分布。
-
其他描述性统计方法:
- 正太分布有两个特性:
- 均值 = 中位数 = 众数
- ‘68-95-99.7规则’ 或者叫 ‘三\(\sigma\)原则’:
- 68%的数据落在平均值加减一个标准差内
- 95%的数据落在平均值加减两个标准差内
- 99.7%的数据落在平均值加减三个标准差内
可以通过这个方法做一个初步的判断
- 正太分布有两个特性:
3.2 盒须图(Box Plot) #
- 盒子中间的线是中位数,盒子的底部和顶部分别是25%分位和75%分位,晶须底部和顶部分别是最小值和最大值
- 盒须图可以帮助我们理解数据的范围和分布情况,并且在比较不同组之间的数据时提供了一些参考
- 盒须快照: 指在某个特定时间点或条件下画出盒须图。
- 中位数:比较每组数据的集中程度
- 四分位数:比较每组的分散程度
- 盒须范围(Interquartile Range,IQR):即Q3 和 Q1 之间的距离。IQR 提供了数据集中 50% 观察值的范围,是衡量数据分布的一个重要指标。
- 最大值和最小值:了解每组数据的整体范围
- 异常值:出现的一些极端情况或者异常情况,需要进一步关注和分析
3.3 二项分布 #
- 单个的二元事件(Binary Event)是伯努利分布,多个伯努利分布就服从二项分布(Binomial Distribution)
- 正态近似:
- 对任何p值,如果p值不变而n(试验次数,或样本容量)增大,得到的均值为np和方差为npq的二项分布在形状上越来越近似一个的正态分布。
- 根据统计学的经验:当np或者nq大于等于5时,才可以使用二项分布的正态近似。更严格一点就是np>5且nq>5。(想要p接近0.5,或者n越大)
3.4 中心极限定理 #
对于独立并同样分布的随机变量,即使原始变量本身不是正态分布,随着样本量的增加,标准化样本均值的抽样分布也会趋向于标准正态分布.
- 在样本量足够大的前提下并满足前提条件时,变量的均值分布会趋向于正态分布,而与该变量所在总体的分布无关。
- 在AB实验中,我们的样本量通常会大于30,当满足独立、来源于同一个分布、以及随机性时,可以通过样本符合正态分布来进行统计学检验。
3.5 大数定理 #
样本数量越多,样本均值会越来越接近总体均值;样本数量越多,样本计算出的频率会越来越接近事件发生的概率。
- 伯努利大数定理:从定义概率的角度,揭示了概率与频率的关系,当N很大的时候,事件A发生的概率等于A发生的频率。
- 辛钦大数定理:揭示了算术平均值和数学期望的关系
- 切比雪夫大数定律:揭示了样本均值和真实期望的关系
3.6 辛普森悖论 #
几组不同的数据中均存在一种趋势,但当这些数据组合在一起后,这种趋势消失或反转。
其产生的原因主要是数据中存在多个变量。这些变量通常难以识别,被称为“潜伏变量”。潜伏变量可能是由于采样错误造成的。
辛普森悖论是一个统计学中的悖论,描述了一个看似矛盾的现象:在对数据进行分组分析时,观察到的总体趋势与分组后趋势相反或者完全不同。
例子:
某大学由两个学院组成。1号学院的男生录取率是75%,女生录取率49%,男生录取率高于女生;2号学院男生录取率10%,女生录取率5%,男生录取率同样高于女生。问:综合两个学院来看,这所大学的总体录取率是否男生高于女生?
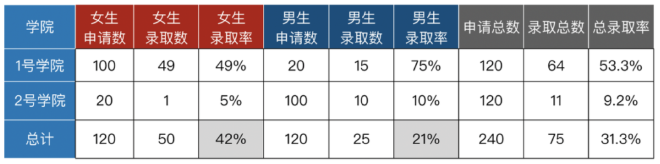
从上表可以看出,尽管两个学院男生录取率都高于女生,但综合考虑两个学院的情况时,男生的总体录取率却要低于女生。这种现象在统计学中被称为辛普森悖论。在A/B实验中,如果实验组和对照组的样本流量分布不一致,就可能产生辛普森悖论,得到不可靠的实验结果。
常见的错误分流:
- 实验中,在不同的渠道/应用市场中,发布不同版本的APP/页面,并把用户数据进行对比;
- 简单地从总体流量中抽取n%用于实验,不考虑流量分布,不做分流处理(例如:简单地从总体流量中任意取出n%,按照ID尾号单双号把用户分成两组)。

